Introduction
The internet of things (IoT) is a term used to describe the ever-growing network of connected devices. These devices can range from simple objects like light bulbs and thermostats to more complex machines like cars and airplanes.
The potential for IoT is vast, and businesses are starting to take notice. Current projections for IoT spending are expected to reach $1.1 trillion US by 2023, with the smart home market alone accounting for over $125 billion US.
Before you get started on an IoT development, it's essential to understand the basics of what makes up an IoT project.
- IoT projects are different from regular IT projects in a few ways:
- Because IoT devices are constructed using both hardware and software components, IoT projects require deep expertise in both fields.
- Hardware and software are developed in tandem, so a mistake in either area can have serious consequences.
- IoT projects require a different kind of testing and validation process. The complexity of IoT devices means that there is a more significant potential for things to go wrong during development and deployment.
- Traditional IT projects are typically planned, designed, developed, tested, and deployed within a relatively short time frame.
- IoT projects could be much longer in scope, with devices being added and changed constantly. This means that the project management and development process must be able to adapt to changes on the fly.
- One of the most important aspects of an IoT project is security. With so many devices connected to the internet, it's more important than ever to make sure that your data is safe from attack.
Despite these challenges, the potential benefits of IoT make it well worth the effort. This article will outline the steps you need to take to get your IoT project off the ground and outline any risks you might face.
1. Where to start?
When developing software, it's important to clearly document your needs. This makes sure that the development team has a good understanding of what you're looking for in their designs and implementation efforts so they can meet all requirements with ease while maintaining budget constraints too!
The first step towards this goal is the creation of a Software Requirements Specification (SRS) document. This document should describe the features and functions of the software you're looking for in detail, as well as how it'll be expected to function. If you need a template to help you get started on an SRS for your IoT project, feel free to contact us.
Once the SRS is complete, you'll need to start thinking about what devices or platforms you'll need to use to bring your idea to life. If you have a good understanding of your target audience and their needs, this process will be much easier. By partnering with an IT vendor with skills in this area, you're much more likely to achieve success. We discussed finding the right IT vendor in a previous article, so if you're not sure where to start, that's a great place to begin.
Based on your SRS, your selected vendor can work with you to determine if your ideas are possible. Next, you'll develop a prototype and test it with your target audience. This will help you determine whether your idea is suitable for a larger commercial market. After that, it's time to start developing the actual product.
2. What is the process of IoT project development?
To make sure that your project development goes smoothly and without any hiccups, it's important you go through a Research & Development (R&D) phase. The R&D phase helps to make sure that you are confident in your designs and specifications and identify potential problems early on that can be solved with extra time or resources.
A successful design starts from understanding what it needs, not just creating something for the sake of getting started!
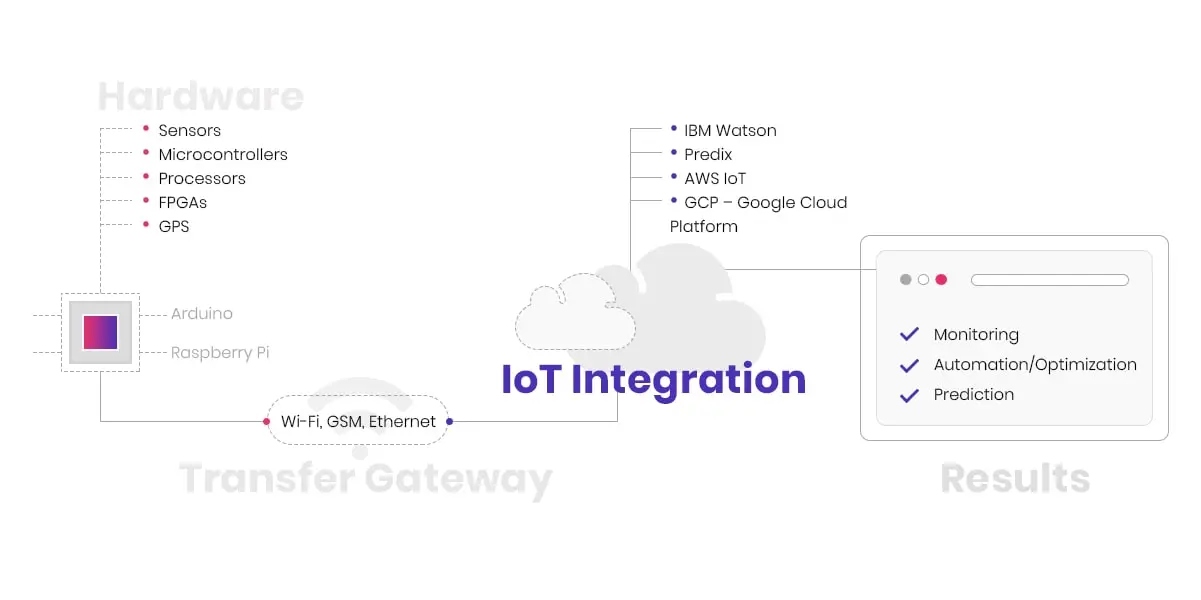
There are four primary phases to consider as part of this process, and they include the following:
2.1 Investigation
In the investigation step, the vendor will help you select a platform and tools that best fit your needs based on your goals and objectives. This includes the selection of a framework and the underlying platform and tools.
Software:
When selecting software for an IoT project, make sure to choose something that's scalable so that it can handle increased traffic as your project grows. You'll also want to look for software that has broad support for a variety of devices, as well as the ability to easily add new ones.
Сonnectivity method:
What kind of connection does your Internet of Things device need? Is it Wi-Fi, Ethernet, USB, or Bluetooth? Is this something that will change as your company expands? These factors should be carefully considered because they may have an impact on the success of your product.
Framework:
The choice of the framework can significantly impact the whole development process, so it's important to research several options before making any final decisions about how things are going to be set up.To serve in this decision, consider previous successful IoT projects and the frameworks that were used there. The right framework will grow with you and can serve you well into the future.
Hardware:
The hardware you choose for your IoT project will depend on the sensors and devices you need to connect. Be sure to select a platform that has broad support for a variety of devices, as well as the ability to add new ones down the road easily.
When prototyping, does it make a difference which development kit you use? It certainly does. Let's look at the differences between three of the most well-known ones.
| Characteristic | Raspberry Pi | Arduino | LattePanda |
|---|---|---|---|
| Definition | Raspberry Pi is a credit-card sized single-board. It displays all the data to a monitor, and you can use standard keyboard and mouse to operate it. | Arduino is a microcontroller motherboard. Basically, it is a simple computer that can run only one program at a time. The biggest plus is that it is very easy to use. | Single board computer. It is conceptually similar to the Raspberry Pi, but is significantly more expensive and runs Intel processors instead of ARM. It is capable of running Windows 10 or Linux. |
| Connectivity Abilities | Can be connected to Bluetooth and the Internet (by Ethernet or Wi-Fi). | Arduino uses additional shield to connect to Bluetooth and Internet. | Bluetooth and the Internet (by Ethernet or Wi-Fi) are both possible connections. |
| Programming languages | Python, C, C++, Java, Scratch, and Ruby | C, C++ | Python, C, C++, Java, Scratch, and Ruby |
| Area of usage | Intense calculations, performing multiple tasks. | Simple and repetitive tasks (e.g. reading environmental data and sending it to social media pages, opening and closing door etc.) | Intensive calculations, performs many tasks simultaneously. |
| Price | $35-40 | $10-20 | $130 - 500 |
2.2 Proof Of Concept
Once you have your tools in place, it's time to get started on development. You'll want to create prototypes and test them with different stakeholders to get feedback. By doing this early on, you can catch potential problems and correct them before they become too costly.
Your proof of concept or POC needs to show that your "idea has legs" and that it'll be a practical option for your business. If its a new technology or service, you'll need to make sure that there is a market for it. You don't want to spend months or years developing a product that no one wants to buy.
2.3 Prototyping
Assuming that the POC is successful, you'll then need to start development in earnest. This will involve creating detailed designs and specifications and working with the development team to make sure that everything is accounted for.

*Prototype of UBreez box developed by Indeema Software
When building your prototype you need to make sure that it addresses the following areas:
- Delivers Value: The prototype needs to provide value to the customer or business in some way. It could be increased efficiency, cost savings, improved user experience or something else.
- MVP: The prototype doesn't need to meet all of the requirements that were outlined in the SRS document. At this early stage you can build a minimal viable product or MVP that showcases the key features of the final product.
- Usability: Make sure that you test the usability of your prototype. This is especially important if you're building a consumer-facing product.
- Is Secure: The prototype must be secure against attacks and unauthorized access.
- Is Testable: The prototype must be easy to test and debug.
2.4 Project Specifications
The detailed requirements document includes all the necessary information to understand what your team needs for you to meet client expectations.
This is a general overview of how one might approach the development and administration of IoT projects. There are many more steps than just these, but they provide an idea of what you should aim to accomplish in your project's early stages.
3. What risks may you face at the beginning of the project?
The development process can be long and arduous, but it's essential to take the time to do it right. If you cut corners, you'll likely end up with a product that doesn't meet your needs or expectations.
Indeema Software, with their experience in the field, eliminates significant risks to make sure that your projects get completed on time. However, for clients new to software development, there are some risks that need to be understood.
3.1 An incompetent specialist or a team that isn't the right fit
Designing for the future starts with a well-rounded UI/UX design that's oriented toward tomorrow's users. If a company or individual is selected with only limited skills, their inexperience might result in a subpar design or implementation.
3.2 The project's structure is inaccurate, and the process is inefficient
IoT projects tend to be complex, with many different components that need to work together. Without a comprehensive understanding of the project's structure, it can be difficult to keep track of individual tasks and their dependencies. As a result, the project can quickly become inefficient and even unmanageable.
3.3 Poor communication
This is probably the most common issue in software development. The client often doesn't clearly understand what they want or needs change during the development process. This can lead to misunderstandings and costly delays.
3.4 Neglecting security
Security should always be a top concern when developing software, but it's especially important in IoT projects. Hackers are increasingly targeting connected devices, so it's essential to protect your data and infrastructure. In an upcoming article, we'll cover how our team guarantees security in IoT projects. Sign up for updates to learn more!
These are just some of the most common mistakes made by businesses starting IoT projects. By avoiding these mistakes, you'll increase your chances of success and avoid costly setbacks.
Conclusion
The challenge for most businesses is that they don't have the in-house expertise to take on an IoT project from start to finish. That's where our team can help. We have experience in all aspects of IoT development, from strategy and planning to execution and delivery. We'd be more than happy to discuss your specific needs and see how we can help. Simply contact us and we'll get started.
Maintaining an in house development process takes time away from core responsibilities which could negatively impact profits so instead leverage outside talent for more efficient results with lower risk involved due to familiarity.
Developing an IoT product can be a daunting task, but by following these simple steps, you'll be on your way to bringing your innovative idea to market. For more information on developing IoT products, contact us today. We're happy to help!
Related: The Benefits of Digitalization for Your Business


